Психрометр Августа

Задание №4 Мистер Джонс.Продолжение

Задача №1

Мистер Джонс очень любит заниматься спортом.
Каждое утро он любит устраивать пробежку.
Поначалу он бежит с одинаковой скоростью 2 м/с. Через 20 секунд после начала своей пробежки,мистер Джонс ускоряется на 2м/с^2. Через 7 секунд, мистер Джонс замедляет темп на 1,5 м/с^2.
Посчитать скорость Мистера Джонса через 30 секунд после начала движения.
Какие типы движения совершает мистер Джонс?

 Решение:

весь путь мистера Джонса можно разделить на три участка:1 участок - равномерное движение(V01=Vx1=2м/с(ах1=0 м/с);t1= 20c), 2 участок -равноускоренное движение(V02=Vx1=2м\c(ах2=2м/с^2);t2=7c;Vx2=V02+ax2t=2+2*7=16м\c), 3 участок - равнозамедленное движение(V03=Vx2=16м\c(ах3=-1,5м/с^2);t3=3c;Vx3=V02+ax2t=16-1,5*3=11,5м\c)

Задача №2

Лучший друг мистера Джонса - медвед, решил сыграть со своим  другом в гонки!
Но мистер Джонс решил схитрить и побежал раньше медведа на 2 секунды, имея на 4 секунде скорость 4 м/с.
Медвед хотел перегнать мистера Джонса, поэтому его ускорение было равно 2 м/с
Какова скорость у друзей на 8 секунде?Какую скорость имел медвед на 6 секунде?

 

Решение:

ускорение мистера Джонса:ax=(Vx-V0)|t=4|4= 1м/с^2

скорость мистера Джонса на 8 секунде:Vx=ax*t=1*8=8м/c

ускорение медведа:ax=2м/с^2

скорость медведа на 8 секунде(не забудьте учесть,что медвед начал свое движение на 2 секунды позже мистера!следовательно считать его скорость будем на 6 секунде его движения):Vx=ax*t=2*6=12м/c

 Задача №3 

Мистер Джонс спешит в гости к своему другу мистеру Смиту. Дом мистера Смита находится в 500 метрах от дома мистера Джонса. Приглашение было на 17:00 часов,однако из-за своей забывчивости мистер Джонс выбежал из дома в 16:55. С каким ускорением  мистер Джонс побежал к мистеру Смиту ,если начальная его скорость была 2м/с? Успел ли мистер джонс к мистеру Смиту?

Решение:

Sx=500m;

tx=4min=4*60c=240c

V0=2m\c

Vx=0

найдем ускорение мистера Джонса:

Sx=((Vx)^2-(V0)^2)\2ax

ax=((Vx)^2-(V0)^2)\2Sx

ax=(0^2-2^2)\2*500=-0,004m\c^2

найдем время, которое потребовалось мистеру Джонсу,чтобы добраться в гости:

(Iсп.)t=(Vx-V0)\ax=-2\-0,004=500c

(IIсп.)Sx=V0t+(ax*t^2)\2

500=2t-0,004*t^2)\2

0=500-2t+0,002t^2

D=4-2000*0,002=4-4=0(1 корень)

t=2\0,004=500c

выясним хватит ли времени мистеру Джонсу:240-500=-260 - на 260 секунд(4 минуты 20 секунд) мистер Джонс опоздал в гости 

Задание №3 Очаровашка Mr.Jones

Задача №1
Mr. Jones вышел на прогулку из своего шикарного дома в лес со скоростью 1м/с.
задача:
- определить путь,пройденный Mr. Jones и время,потраченное Mr. Jones на путь из дома в лес.
- составить уравнение движение Mr. Jones при равномерном движении.
- определить через какой промежуток времени (в секундах) Mr. Jones пройдёт через точку отсчета

Задача№2

Mr. Jones забыл дома свой кошелек,не отчаиваясь он решил за ним вернутся поскорее домой.
Определить:

-по графику начальную точку положения объекта(Mr. Jones)

-кол-во времени потраченное на путь до дома

- уравнение движение Mr. Jones при равномерном движении.

- в какой точке будет находится объект через 4 с движения.

Задача№3

Mr. Jones случайно наткнулся на медведа и тот его заметил.Mr. Jones испугался и бросился бежать от медведа в сторону дома.
однако несмотря на удивительное везение Mr. Jones,медвед его все же догнал...

Задача:
-Определить скорость Mr. Jones,если известно,что до точки с координатой +1 он добежал за 2  секунды(х0=-5)

-Определить скорость медведа,если известно,что до точки с координатой -4 он добежал за 1 секунду(х0=-9)
-Определить место и время встречи медведа и Mr. Jones

Решения задач
Задача №1
- определить путь,пройденный Mr. Jones и время,потраченное Mr. Jones на путь из дома в лес:
S=7,5+8=15,5 m
t=S:V; t=15,5:1=15,5 сек
- составить уравнение движение Mr. Jones при равномерном движении:
X0=7,5;Vx=1m/с;
X=X0+Vxt
X=7,5+t;
- определить через какой промежуток времени (в секундах) Mr. Jones пройдёт через точку отсчета:X=7,5+t;0=7,5+t;
t=7,5 сек


Задача №2

Определить:

-по графику начальную точку положения объекта(Mr. Jones)
X0=-2,5;

-кол-во времени потраченное на путь до дома
X=X0+Vxt;
Х0=-2,5;
Vx=2 m/c
X=8;
8=-2,5+2t
2t=-10,5
t=5,25 сек

- уравнение движение Mr. Jones при равномерном движении.
X=X0+Vxt
X=-2,5+2t

- в какой точке будет находится объект через 4 с движения.
X=-2,5+2*4;
X=5,5 m


Задача №3

-Определить скорость Mr. Jones,если известно,что до точки с координатой +1 он добежал за 2  секунды(х0=-5):
Vx=(X-X0)/t;
X0=-5;
X=1;
t=2;
Vx=(1+5)/2;
Vx=3 m/c;

-Определить скорость медведа,если известно,что до точки с координатой -4 он добежал за 1 секунду(х0=-9):
Vx=(X-X0)/t;
X0=-9;
X=-4;
t=1;
Vx=(-4+9)/1;
Vx=5 m/c;

-Определить место и время встречи медведа и Mr. Jones:
X1=X2;
X1=-5+3t;
X2=-9+5t;
-5+3t=-9+5t;
4=2t;
t=2 сек-(время встречи)
X=-9+5*2=-5+3*2;
X=1 m(место встречи)

Кинематика Задание№2

«Определение проекций вектора на оси»

Вариант №10

Цель:

·                     определить координаты начало и конца каждого вектора

·                     определить проекции  векторов на оси

·                     определить длину векторов

·                     определить сумму и разность двух предложенных векторов

(рис.1)

1.Определим координаты точек начала и конца векторов AB(a) и CD(b), представленных на изображении (рис.1):

А(6,5;1);В(3,5;-0,7)
С(-1;-3);D(-1;2)

2.Найдем длину проекций векторов АВ(а) и DC(b):

АВ(a) : Sx =x-x0; Sx=3,5-6,5=-3; Sy=y-y0; Sy=-0,7-1=-1,7;

DC(b) : Sx =x-x0; Sx=-1+1=0; Sy=y-y0; Sy=2+3=5;

3.Вычислим длину векторов a и b по формуле:

|S| = sqpt(Sx^2 + Sy^2)

a=3,44  и b=5

Вывод: длина вектора a равна 3,44, длина вектора b равна 5.

4.Определим сумму и разность двух предложенных векторов a и b. Разностью будет являться отрезок S₁ (B₁C) суммой – S₂ (B₃C) (рис.1).

B₁(-4;0,4);C(-1;-3)

B₃(2;3,6);С(-1;-3)

5.Найдем длину проекций векторов S₁ (B₁C) и S₂ (B₃C):

S1 (B1C): Sx =x-x0; Sx=-1+4 =3; Sy=y-y0; Sy=-3-0,4=-3,4;

S2 (B3C): Sx =x-x0; Sx=-1-2=-3; Sy=y-y0; Sy=-3-3,6=-6,6;

6.Вычислим длину векторов S₁ (B₁C) и S₂ (B₃C) по формуле:

|S|=sqpt(Sx^2 + Sy^2) |S₁ (B₁C)| = sqpt(3^2 + (-3,4)^2)=4,5

|S₂ (B₃C)| = sqpt((-3)^2 + (-6,6)^2)=7,24 

Вывод: длина вектора S₁ (B₁C) равна 4,5, длина вектора S₂ (B₃C)  равна 7,24.

Конечные результаты:

1.     координаты начала и конца каждого вектора:

А(6,5;1);В(3,5;-0,7)
С(-1;-3);D(-1;2)

2.определить длину векторов:

a = 3,44, b= 5.

3.сумма и разность двух предложенных векторов:

S₁ = 4,5, S₂ = 7,24.

Кинематика Задание№1

«Определение перемещения божьей коровки(БК)»

Цель работы: определение проекции начала и конца перемещения на координатных осях, определение проекции перемещения и величины самого перемещение БК, сравнение пути и перемещения БК.

(рис.1)

Результаты измерения: на представленном мной изображении (рис.1),имеется траектория движения объекта (БК). Начальной точкой положения объекта является точка А (3,2;-2,5),конечной точкой является точка В (1,6;0,3).по данным условиям можно определить проекции по оси х и у:

S_x =x-x₀;

S_x=1,6-3,2=-1,6;

S_y=y-y₀;

S_y=0,3+2,5=2,8;

Вычислим теперь перемещение объекта (АВ) по формуле:|S| = sqpt(Sx^2 + Sy^2)        |S| = sqrt((-1,6)^2 + (2,8)^2) = sqrt(10,4)=3,22

Перемещение объекта БК равно 3,22 

Вывод: на изображении (рис.1) очевидна разница между величинами пути (l) и перемещением (S) объекта (БК)

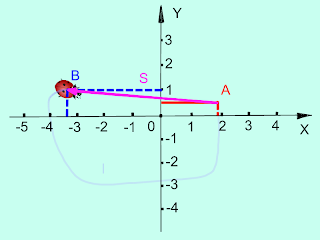
(рис.2)

Результаты измерения: на представленном мной изображении (рис.2),имеется траектория движения объекта (БК). Начальной точкой положения объекта является точка А (1,9;0,5),конечной точкой является точка В (-3,4;1).по данным условиям можно определить проекции по оси х и у:

S_x =x-x₀;

S_x=-3,4-1,9=-5,3;

S_y=y-y₀;

S_y=1-0,5=0,5;

Вычислим теперь перемещение объекта (АВ) по формуле:

|S| = sqpt(Sx^2 + Sy^2)        |S| = sqrt((-5,3)^2 + (0,5)^2) = sqrt(28,34)=5,32

Перемещение объекта БК равно 5,32

Вывод: на изображении (рис.2) очевидна разница между величинами пути (l) и перемещением (S) объекта (БК)

(рис.3)

Результаты измерения: на представленном мной изображении (рис.3),имеется траектория движения объекта (БК). Начальной точкой положения объекта является точка А (-2,9;-2,1),конечной точкой является точка В (3;0,6).по данным условиям можно определить проекции по оси х и у:

S_x =x-x₀;

S_x=3+2,9=5,9;

S_y=y-y₀;

S_y=0,6+2,1=2,7;

Вычислим теперь перемещение объекта (АВ) по формуле:

|S| = sqpt(Sx^2 + Sy^2)        |S| = sqrt(5,9)^2 + (0,5)^2) = sqrt(42,1)=6,48

Перемещение объекта БК равно 6,48

Вывод: на изображении (рис.3) очевидна разница между величинами пути (l) и перемещением (S) объекта (БК)